QNH Determination (Relationship between QNH and station pressure)

[MSFS 2020] Questions & Community Discussions Aircraft
1

I hate to bring this back up again after so much work has been done to improve
it, but I still see an important issue with it. There appears to be something
wrong with the relationship between QNH and the ambient pressure at that
location. As an example, I located the airplane at a high elevation airport
(SLLP) in La Paz, Bolivia. Using real weather the METAR indicated a QNH of
1037. The altitude simulation variables are shown in the following screenshot:

767×483 29.3 KB
As you can see, it gives an
ambient pressure at the airport of 635.45 hPa for the QNH of 1037 and airport
elevation of 13,313 ft. However, for that elevation and QNH, the ambient
pressure should be 627.57 hPa. The MSFS pressure leads to a pressure altitude
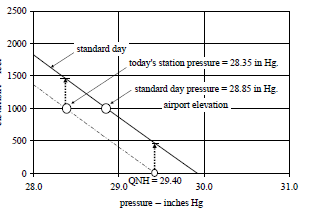
of 12,355 ft, but it should really be 12,670 ft. A QNH of 1037 should shift
the pressure vs altitude curve down by 642.5 ft. If the ambient pressure is
really 635.45 hPa at the field elevation of 13,313 ft, then the QNH should be
1048.8. My calculations are based on the following equations from the Boeing
Jet Transport Performance Methods document (with 1013.25 hPa substituted for
29.92 in Hg as the sea level pressure).

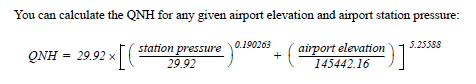
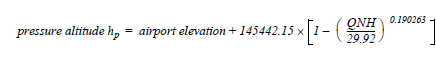This is a stumbling block for us
in trying to implement the effect of barometric pressure compensation since
what we would be basing it on (the equations above) are different than what
MSFS appears to be using.

2

Hi there, The sim uses the NASA Standard ISA Atmosphere 1976 formulae
(1976_Std_Atm_NASA-TM-X-74335.pdf
) (also adopted by ICAO) to compute altimetry. Using the tables I see in the
official paper on pages 187 and 188 to cross-check the sim formulae, I see
635.45mb corresponding to a pressure altitude of roughly 3766m (~12355.6ft),
and 13313ft (~4057.8m) corresponding to an ambient pressure of 611.8mb. The
difference between the two pressures is thus 23.65mb, leading to a required
QNH of 1013.25 + 23.65, or 1036.9mb. I am also able to validate these numbers
using the various ISA standard atmosphere calculators available online. I
cannot seem to validate the Boeing formulae using any ISA standard atmosphere
sources I can find, so I’m not totally sure where they are deriving from. Hope
that helps! -Matt

3

Hi Matt, Thank you for responding. I have no qualms with the pressure vs
pressure altitude relationship in MSFS (at least since it was cleaned up). I
agree that 635.45 mb corresponds to a pressure altitude of about 12355 ft and
that 611.8 mb corresponds to a pressure altitude of about 13312 ft. What I
fail to see is why you are referencing the 635.45/12355 value. That’s not
where the airplane (or the station is). You seem to be calculating a QNH
correction as simply being a delta p along the pressure vs altitude line
whereas it is really a sea level equivalent pressure change that results in
the same number of feet difference between the station pressure altitude and
the sea level pressure line at the station pressure:
The pressure altitude can be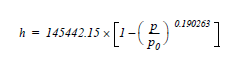
calculated for any pressure from the
equation For example, plug in
635.45 mb and you get 12355 ft. For 611.8 mb you get 13312 ft. In the above
example, with a station pressure of 28.35 in Hg (960 mb), the pressure
altitude is about 1485 ft. It takes a QNH of 29.40 in Hg (999.6 mb) to achieve
that same 485 ft difference between the 1000 ft elevation and the 1485
pressure altitude. If you are given the QNH, then the difference between the
pressure altitude and the elevation can be found by simply inputting QNH as
the pressure in the above equation For the SLLP example I gave then, if the
QNH is 1037, then the difference in pressure altitude is -643 ft. That would
mean the pressure altitude for the La Paz elevation of 13313 ft is 13313-643
=12670 ft. And the corresponding station pressure for that pressure altitude
would be 627.57 mb as I stated above. Regards, Don

4

After looking at this a bit more, I think I see where the issue is. It appears
that you are assuming that pressure vs altitude is completely linear through
the SLLP elevation of 13313 ft. It is not (as you can glean from the pressure
altitude equation I provided). Using your numbers from the 1976 NASA Standard
Atmosphere model, for a pressure of 635.45 mb and altitude of 3766 m, a linear
variation of pressure with altitude would give about 9.97 m/mb. For a pressure
of 611.8 mb and 4057.8m, a linear variation of pressure with altitude would
give 10.11 m/mb. These numbers are not equal. They would be if the variation
of pressure with altitude was linear. Only if the standard pressure variation
is linear with altitude can you use the difference between the pressure at the
station elevation and the standard pressure to add to the sea level standard
pressure to determine the QNH. MSFS does not use a linear variation of
standard pressure with altitude, so why does it appear to be assuming that to
be the case for determining QNH? It might work acceptably well for altitudes
close to sea level, but it breaks down for very high altitude airports like La
Paz. It really falls apart when examining the effect of changing the baro
setting of the altimeter at high altitudes. Sorry for the continued edits, but
I am trying to make things more clear. I changed the title of the
question/issue for that reason. Changing a baro setting in an airplane
altimeter shifts the standard pressure vs altitude curve up or down, not
sideways. The equations provided in the Boeing document are easily derived if
you need for me to provide that information. They should be relatively
straightforward just from inspection.

5

Hi dontsim, Looking only at the code and then also the ISA document had me in
a bit of tunnel vision regarding the formula you provided. I’m not entirely
convinced of the exponent value of the Boeing QNH formula, but that aside (and
it’s a very small difference), you are of course correct. The current sim code
is applying the offset in the wrong area (effectively adding the QNH vs STD
pressure delta through the whole range, instead of offsetting the SL altitude
as you point out) both in the altimeter and in the atmosphere itself. This
internal consistency made this error much harder to spot. We should be able to
get that sorted in both locations for SU9, and I have tested this against the
provided Boeing formula, my own QNH derivation, and other derivations and
calculators available elsewhere. Thanks much for the dialog!

6

Fantastic! As for the exponent in the Boeing equations, the 5.25588 comes from
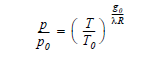where g sub 0 is of course the
sea level standard gravitational acceleration, lambda is the temperature lapse
rate, and R is the specific gas constant. In English units, g sub 0 is
32.17405 ft/sec squared, lambda is 0.00356616 deg F/R per foot, and R is
1716.5619 foot-pounds per slug-degree R. Of course if coding this, there is no
reason to do the multiplication beforehand. You can have the constants
defined, and then use the full g sub 0 over lambda times R to avoid the round-
off. In SI units, for g sub 0 = 9.806665 meters per second squared, lambda =
0.0065 deg C/K per meter, and R = 287.0529 Newton-meters per kg mass-degree K,
I get 5.25589. And then, the exponent 0.190263 is just 1/5.25588.